Lửa thiêng (Huy Cận) là một trong những tác phẩm đạt được giải thưởng văn học. Tập thơ là nỗi tiếc nuối những điều đẹp đẽ ngày xưa. Bài viết hôm nay, chúng ta sẽ cùng hòa mình vào những vần thơ hay này để cảm nhận dòng chảy tâm tư của tác giả nhé. […]
Top những bài thơ Nguyễn Bính về quê hương, mùa xuân, tình yêu hay nhất
Những bài thơ Nguyễn Bính về quê hương, mùa xuân, tình yêu đã được rất nhiều bạn đọc yêu mến. Ở trong thơ ông người ta tìm thấy cái chất riêng, một phong cách rất riêng, không trộn lẫn. Nguyễn Bính là một trong những nhà thơ nổi tiếng đình đám ở nước ta vào […]
Phân tích nhân vật lão Hạc trong truyện ngắn Lão Hạc của Nam Cao
Phân tích nhân vật lão Hạc trong truyện ngắn Lão Hạc của Nam Cao để thấy được số phận con người trong xã hội cũ. Một cuộc đời cô đơn bất hạnh để rồi chết trong đau đớn của lão nông nghèo khổ đã khiến lay động biết bao nỗi xót thương. Cùng PUD tìm […]
Trở Về Với Mẹ Ta Thôi (Đồng Đức Bốn) – Bài thơ cảm động nhất
Trở Về Với Mẹ Ta Thôi là một bài thơ chứa đựng nhiều cảm xúc của nhà thơ Đồng Đức Bốn. Đây là một thi phẩm giá trị chạm bài trái tim bạn đọc sâu sắc khi bày tỏ sự biết ơn cùng lòng thương xót cho người mẹ cả một đời hi sinh cho […]
1001 bài thơ về áo dài Việt Nam hay và đặc sắc nhất
Những bài thơ về áo dài luôn được đông đảo các bạn đọc yêu quý bởi đây là một biểu tượng độc đáo trong văn hóa của người Việt. Trong chùm thơ này có nhiều điều khiến người ta yêu thích chính là áo dài trắng gợi cảm xúc của một thời cắp sách tới […]
Cách dạy trẻ học thuộc bảng cửu chương nhanh chóng và hiệu quả
Dạy trẻ học thuộc bảng cửu chương là kĩ năng rất quan trọng không chỉ của giáo viên mà còn của các bậc phụ huynh.Bảng cửu chương đóng vai trò quyết định trong việc tính toán.Bảng cửu chương còn trang bị cho trẻ những kỹ năng tính toán nhanh sẽ theo trẻ suốt thời gian […]
Bài Thơ Ở Hai Đầu Nỗi Nhớ – Trần Đình Chính Đặc Sắc Nhất
Bài thơ Ở Hai Đầu Nỗi Nhớ của nhà thơ Trần Đình Chính chính là tác phẩm đầu tay của ông. Bài thơ chính là tiếng lòng mối tình đầu của ông dành cho một cô sinh viên Sài Gòn. Với lời thơ thấm đẫm tình cảm da diết, nồng nàn mà tác phẩm đã […]
Những bài thơ Hàn Mặc Tử hay nhất “sống” mãi cùng thời gian
Những bài thơ Hàn Mặc Tử hay nhất là tuyển tập thơ nổi tiếng nhất trong cuộc đời sáng tác của ông. Hàn Mặc Tử tên thật là Nguyễn Trọng Trí được mọi người biết đến với những dòng thơ lãng mạn hiện đại, ông là khởi nguồn của dòng “thơ điên”.Hàn Mặc Tử nổi […]
Phân tích nhân vật Từ Hải trong đoạn trích Chí khí anh hùng hay nhất
Nhân vật Từ Hải trong đoạn trích Chí khí anh hùng hiện lên là một chàng trai lịch lãm, có tư chất, có phong cách, chuộng nghĩa. Con người ấy đến từ một giấc mơ và ở lại như một huyền thoại; hiện diện trong “Truyện Kiều” như một nhân cách sử thi. Cùng tìm […]
Thủy triều là gì? Giờ thủy triều lên xuống trong ngày?
Thủy triều là gì? Giờ thủy triều lên xuống trong ngày? là thắc mắc của đông đảo bạn đọc. Thủy triều là một hiện tượng tự nhiên diễn ra hằng ngày. Để giúp các bạn có thể hiểu hơn về hiện tượng này thì ngay bây giờ chúng ta hãy cùng nhau tham khảo bài viết […]
Tại sao người Indonesia trùm đầu? Giải đáp chi tiết nhất
Nếu có dịp đến thăm Indonesia hay các quốc gia Hồi giáo khác, chắc hẳn bạn đã phần nào quen thuộc với hình ảnh những người phụ nữ trùm khăn kín đầu. Bạn đã bao giờ thắc mắc tại sao người Indonesia trùm đầu chưa? Hãy cùng chúng tôi khám phá những bí mật đằng […]
Công thức xoay rubik 3×3, giải đố nhanh, chính xác nhất
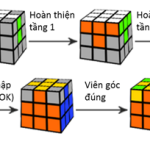
Rubik là gì? Công thức xoay rubik 3×3 như thế nào đơn giản, chính xác nhất? Rubik là trò chơi giải đố mang tính giải trí cao, kích thích sự phát triển trí não, được nhiều người yêu thích đặc biệt đối với thế hệ trẻ. Bài viết hôm nay, chúng ta sẽ cùng nhau […]
Tìm Hiểu Luật Chơi Tiến Lên Miền Nam Chi Tiết Nhất
Tiến Lên Miền Nam (hay còn gọi là TLMN) là một trong những game đánh bài được yêu thích nhất tại Việt Nam. Nó có nguồn gốc từ miền Nam Việt Nam và trở nên rất phổ biến vào những năm 1970. Trò chơi này đòi hỏi kỹ năng tính toán, khả năng ghi nhớ […]
Các Trò Chơi Trong Casino Kích Thích Trí Tò Mò Người Chơi
Casino được biết đến như một “địa điểm” quy tụ nhiều người chơi muốn thử sức với những trò chơi may rủi. Hầu hết các trò chơi trong Casino đều có tính hấp dẫn cao và kích thích trí tò mò của người chơi. Vậy bạn có biết trong Casino có những trò chơi gì […]
Sân Vận Động Bóng Đá Lớn Nhất Thế Giới Công Suất Bao Nhiêu?
Sân vận động bóng đá lớn nhất thế giới ở đâu? Công suất bao nhiêu? chính là điều bạn đang quan tâm. Hãy cùng điểm qua top những sân bóng đá lớn nhất qua bài viết này của chúng tôi Tham quan 5 sân vận động bóng đá lớn nhất Danh sách các sân vận […]