Khoảng cách giữa 2 đường thẳng trong mặt phẳng oxy
Cho 2 đường thẳng chéo nhau:
d1 đi qua A có 1 VTCP
d2 đi qua B có 1 VTCP
Khoảng cách từ điểm M đến đường thẳng d1
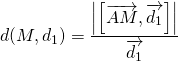
Tính khoảng cách giữa 2 đường thẳng d1 d2
Ví dụ:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
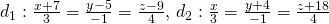
. Tính khoảng cách giữa d1 và d2.
Ta dễ dàng kiểm tra được d1 và d2 là hai đường thẳng song song, nên ta chỉ việc lấy một điểm bất kì thuộc d1, và tính khoảng cách từ điểm đó đến d2.
Ta dễ dàng kiểm tra được d1 và d2 là hai đường thẳng song song, nên ta chỉ việc lấy một điểm bất kì thuộc d1, và tính khoảng cách từ điểm đó đến d2.
Khoảng cách giữa 2 đường thẳng trong oxyz
Cách 1:
Đi qua M1. có 1 VTCP
đi qua M2. có 1 VTCP
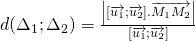
Cách 2:
AB là đoạn vuông góc chung
Ví dụ:
a) CMR: d1, d2 chéo nhau
b) Tính d(d1;d2)
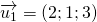
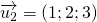
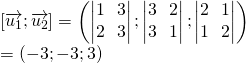
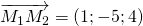
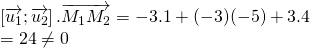
Lời giải:
a)
d1 đi qua M1(1;2;-3), có 1 VTCP
d2 đi qua M2(2;-3;1), có 1 VTCP
Vậy d1, d2 chéo nhau
b)
Cách 1:
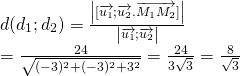
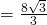
Cách 2:
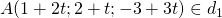
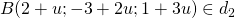
AB là đoạn vuông góc chung
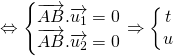
AB = d(d1;d2)
Phương pháp tính khoảng cách giữa hai đường thẳng chéo nhau
Để tính khoảng cách giữa hai đường thẳng chéo nhau ta có thể dùng một trong các cách sau: Dựng đoạn vuông góc chung MN của a và b. Khi đó dleft( {a,b} right) = MN. Sau đây là một số cách dựng đoạn vuông góc chung thường dùng :
Phương pháp 1: Chọn mặt phẳng (α) chứa đường thẳng ∆ và song song với ∆’. Khi đó
Phương pháp 2: Dựng hai mặt phẳng song song và lần lượt chứa hai đường thẳng. Khoảng cách giữa hai mặt phẳng đó là khoảng cách cần tìm.
Phương pháp 3: Dựng đoạn vuông góc chung và tính độ dài đoạn đó.
Trường hợp 1: ∆ và ∆’ vừa chéo nhau vừa vuông góc với nhau
Bước 1: Chọn mặt phẳng (α) chứa ∆’ và vuông góc với ∆ tại I
Bước 2: Trong mặt phẳng (α) kẻ .
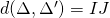
Khi đó IJ là đoạn vuông góc chung và .
Trên đây chúng tôi đã chia sẻ đến các bạn công thức tính khoảng cách giữa hai đường thẳng đầy đủ và chính xác nhất. Qua đó các bạn sẽ dễ dàng giải những bài tập trong sách giáo khoa và áp dụng được nhiều trong cuộc sống. Hy vọng các bạn sẽ hài lòng với bài viết này của chúng tôi. Thân Ái!