Định lý Talet trong tam giác
Định lý Talet thuận
Nếu có một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ xuất hiện những cặp đoạn thẳng tỉ lệ trên hai cạnh bị cắt đó.
Ta có tam giác ABC, đường thẳng d cắt AB tại D, cắt AC tại E và d song song với BC.
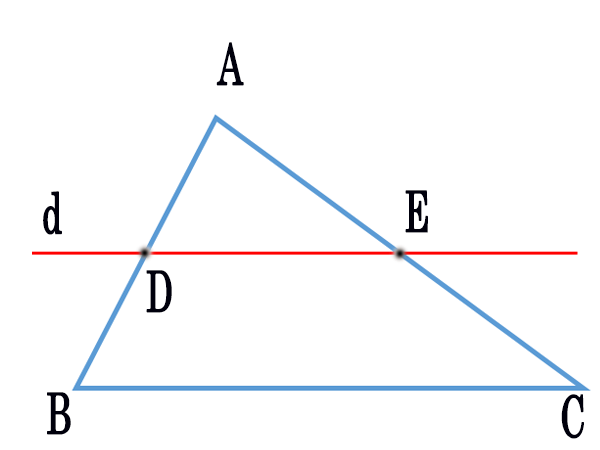
Theo định lý Talet ta được:
ADAB=AEAC và ADDB=AEEC và DBAB=ECAC
Định lý talet đảo
Khi xuất hiện một cặp cạnh tỉ lệ trên hai cạnh của một tam giác thì sẽ xuất hiện trên hai cạnh đó một đường thẳng song song với cạnh còn lại của tam giác.
Lưu ý: Định lý vẫn đúng cho trường hợp đường thẳng cắt phần kéo dài hai cạnh của tam giác.
Với hình minh họa trên, tam giác ABC có ADAB=AEAC hoặc ADDB=AEEC hoặc DBAB=ECAC.
Theo định lý Talet đảo ta được: DE song song với cạnh BC (Ký hiệu: DE//BC)
Hệ quả
Hệ quả 1: Một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới có 3 cạnh tỉ lệ với 3 cạnh của tam giác ban đầu.
Hệ quả 2: Một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì sẽ tạo ra một tam giác mới đồng dạng với tam giác ban đầu.
Hệ quả 3 – Talet mở rộng: Ba đường thẳng đồng quy thì chắn trên hai đường thẳng song song các cặp đoạn thẳng tỉ lệ.
Định lí talet trong hình thang
Nếu có một đường thẳng song song với 2 cạnh đáy của hình thang và cắt 2 cạnh bên của hình thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.
Ví dụ cho hình thang như bên dưới:
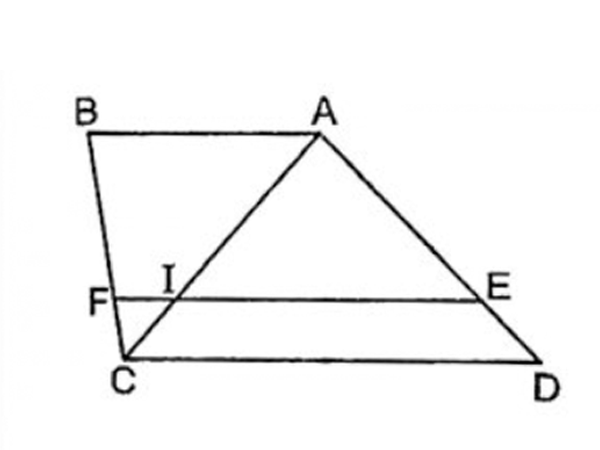
Ta có hình thang ABCD, E thuộc AD, F thuộc BC.
Nếu EF∥AB∥CD, ta có AEDE=BFCF
Ngược lại nếu: AEDE=BFCF. Suy ra EF∥AB∥CD.
Định lí talet trong không gian
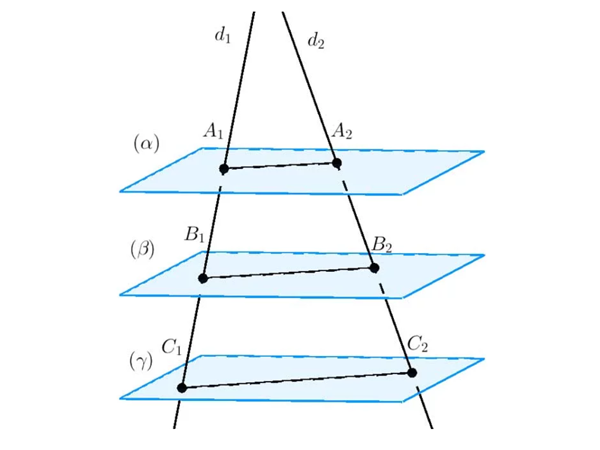
Ba mặt phẳng song song chắn trên hai đường thẳng những đoạn thẳng tỉ lệ A1B1B1C1=A2B2B2C2
Định lý đảo của định lý Talet trong không gian:
Cho 2 đường thẳng d1, d2 chéo nhau và các điểm A1, B1, C1∈d1 và A2, B2, C2∈d2 sao cho: A1B1B1C1=A2B2B2C2
Khi đó các đường thẳng A1A2, B1B2, C1C2cùng song song với một mặt phẳng (đây không phải là mặt phẳng duy nhất)
Một số bài toán ví dụ
Bài tập 1: Cho tứ giác ABCD, đường thẳng đi qua A song song với BC và cắt BD ở E. Đường thẳng đi qua B song song với AD và vắt AC tại G. Yêu cầu:
- Chứng minh EG∥CD
- Giả sử AB∥CD, chứng minh AB2=CD.EG
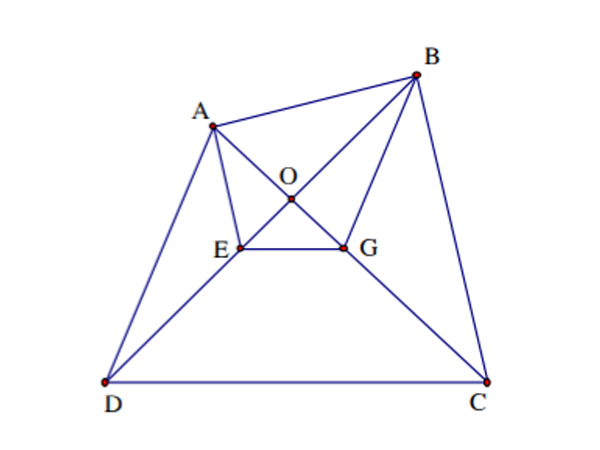
Bài giải:
Gọi O là giao điểm của đoạn AC và BD
- Theo đề bài ta có:
AE∥BC⇒OEOB=OAOC(1)BG∥AC⇒OBOD=OGOA (2)
Nhân (1) và (2) theo vế ta được:
OEOD=OGOC⇒EG∥CD
- Theo giả thiết ta có AB∥CD thì EG∥AB∥CD, BG∥AD
Suy ra ABEG=OAOG=ODOB=CDAB⇒ABEG=CDAB⇒AB2=CD.EG
Bài tập 2: Cho hình bình hành ABCD, đường thẳng a đi qua điểm A và cắt BD, BC, DC lần lượt tại các điểm E, K, G. Yêu cầu:
- AE2=EK.EG
- 1AE=1AK+1AG
- Thay đổi vị trí của đường thẳng a, nhưng vẫn đi qua điểm A thì tích BK.DG có giá trị không đổi.
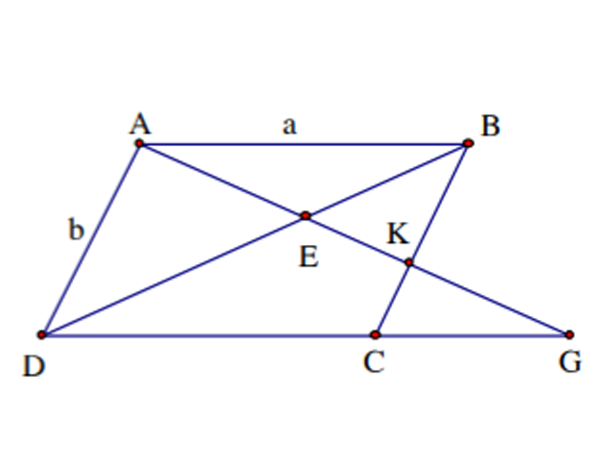
Bài giải:
- Theo giả thuyết ta có ABCD là hình bình hành, điểm K thuộc BC
Suy ra AD∥BK, theo hệ quả của định lý Talet ta có:
EKAE=EBED=AEEG⇒EKAE=AEEG⇒AE2=EK.EG
- Ta có AEAK=DEDB; AEAG=BEBD nên:
AEAK+AEAG=BEBD+DEBD=BDBD=1⇒AE.(1AK+1AG)=1⇒1AE=1AK+1AG (đpcm)
- Ta có BKKC=ABCG⇒BKKC=aCG (1)
KCAD=CGDG⇒KCb=CGDG (2)
Nhân (1) và (2) theo vế ta được:
BKb=aDG⇒BK.DG=ab không đổi vì a =AB, b = AD là độ dài 2 cạnh của hình bình hành ABCD.
Qua bài viết trên đây, hy vọng bạn nắm vững kiến thức về định lí Talet và các dạng bài tập liên quan. Hãy luôn đồng hành cùng PUD để có cơ hội chia sẻ nhiều thông tin hữu ích khác trên các lĩnh vực như văn hoc, toán học, vật lí, hóa học, sinh học, lịch sử, địa lí … bạn nhé !