Làm thế nào để tính diện tích tam giác trong hệ trục tọa độ Oxyz? Bài viết dưới đây sẽ hướng dẫn các bạn cách tính diện tích tam giác trong không gian Oxyz.
Công thức tính diện tích tam giác cấp THPT
Đầu tiên, chúng ta nhắc lại một số công thức tính diện tích tam giác đã biết.
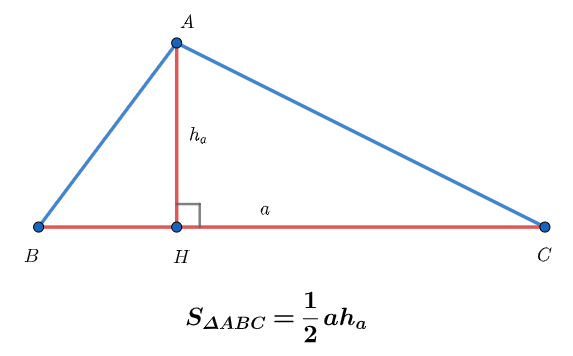
• Tính diện tích tam giác khi biết đáy và chiều cao. Diện tích tam giác bằng nửa đáy nhân với chiều cao.
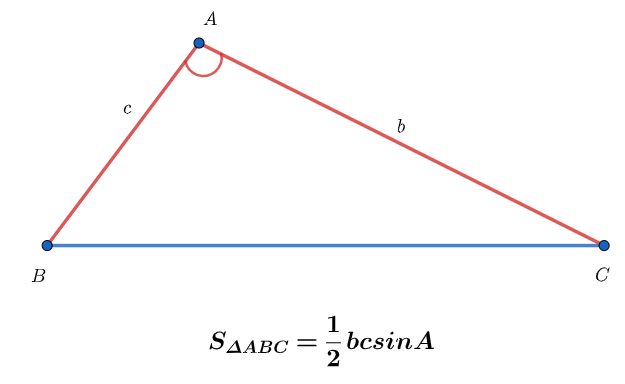
• Tính diện tích tam giác biết hai cạnh và góc xen giữa. Diện tích tam giác bằng nửa tích hai cạnh nhân với sin góc xen giữa
• Tính diện tích tam giác khi biết nửa chu vi và bán kính đường tròn nội tiếp. Diện tích của một tam giác bằng tích của nửa đường tròn và bán kính của đường tròn nội tiếp.
![]()
• Tính diện tích tam giác khi biết độ dài ba cạnh và bán kính đường tròn ngoại tiếp. Diện tích tam giác bằng tích độ dài ba cạnh chia cho 4 lần bán kính đường tròn ngoại tiếp.
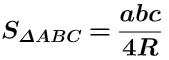
• Tính diện tích tam giác theo công thức Heron:
![]()
trong đó p là nửa chu vi. Và a, b, c là độ dài ba cạnh của tam giác.
Bộ đề trắc nghiệm trực tuyến có lời giải chi tiết: Diện tích tam giác
Công thức tính diện tích tam giác trong hệ tọa độ OXYZ
Về mặt lý thuyết, chúng ta đều có thể sử dụng các công thức trên để tính diện tích tam giác trong không gian hoặc trong không gian Oxyz. Tuy nhiên điều này sẽ gặp một số khó khăn trong tính toán. Vì vậy, trong không gian Oxyz, người ta thường tính diện tích tam giác bằng tích có hướng.
Trong không gian Oxyz, cho tam giác ABC. Diện tích tam giác ABC được tính theo công thức:
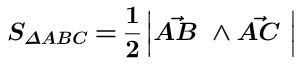
Hình minh họa:
Trong không gian Oxyz, cho tam giác ABC có tọa độ ba đỉnh lần lượt là A(-1;1;2), B(1;2;3), C(3;-2,0). Tính diện tích tam giác ABC.
Câu trả lời:
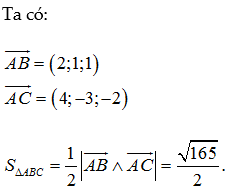
Chúc các bạn thành công!