Lăng trụ tam giác đều là gì?
Lăng trụ tam giác đều được nhắc nhiều trong bộ môn toán học 8. Vậy lăng trụ tam giác đều là gì? Ngay dưới đây, chúng ta sẽ cùng nhau tìm hiểu nhé.
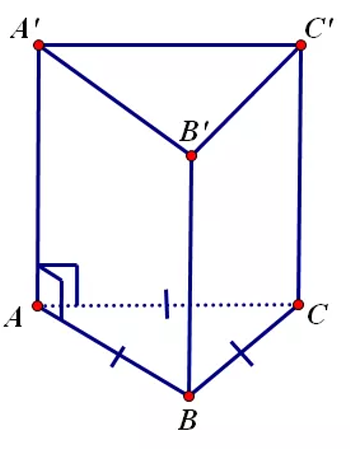
Hình lăng trụ là một đa diện gồm có hai đáy là hai đa giác bằng nhau và nằm trên hai mặt phẳng song song, các mặt bên là hình bình hành, các cạnh bên song song hoặc bằng nhau
Hình lăng trụ tam giác đều là hình lăng trụ có hai đáy là hai tam giác đều bằng nhau.
Tính chất hình lăng trụ tam giác đều
Dưới đây là 3 tính chất hình lăng trụ tam giác đều. Với những tính chất này, bạn sẽ dễ dàng hoàn thành bài tập chứng minh tốt nhất. Cụ thể:
- Hai đáy là hai tam giác đều bằng nhau do đó các cạnh đáy bằng nhau.
- Cạnh bên vuông góc với mặt đáy.
- Các mặt bên là các hình chữ nhật.
Thể tích khối lăng trụ tam giác đều có cạnh bằng a
Thể tích hình lăng trụ bằng diện tích của mặt đáy và khoảng cách giữa hai mặt đáy hoặc là chiều cao. Công thức tính thể tích hình lăng trụ tam giác giác đều
V=B.h
Trong đó:B là diện tích đáy, h là chiều cao của khối lăng trụ, V là thể tích khối lăng trụ
Đáy của hình lăng trụ tam giác đều chính là hình tam giác đều. gọi A là diện tích của tam giác đều ta có công thức tính diện tích tam giác đều như sau:
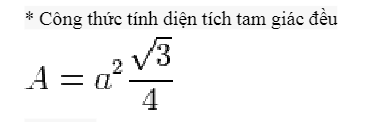
Bài tập lăng trụ tam giác đều
Với lượng kiến thức về hình lăng trụ tam giác đều trên, các bạn cùng chúng tôi tham khảo và giải những bài tập dưới đây nhé.
Bài tập 1:
Tính thể tích khối lăng trụ tam giác đều ABCA’B’C’ có đáy là tam giác nội tiếp trong đường tròn bán kính a, diện tích mặt bên lăng trụ là
Bài tập 2
Lăng trụ tam giác đều ABCA’B’C’ có chiều cao a. Mặt phẳng (ABC’) tạo với mặt đáy góc 300. Tính thể tích khối lăng trụ
Bài tập 3
Lăng trụ tam giác đều ABCA’B’C’ có cạnh đáy là a. Diện tích tam giác ABC’ là bài tập lăng trụ tam giác đều …Tính thể tích khối lăng trụ
Bài tập 4
Lăng trụ tam giác ABCA’B’C’ có đáy ABC là tam giác đều cạnh a. Đỉnh A’ của lăng trụ cách đều A, B, C. Cạnh bên AA’ tạo với mặt đáy một góc 600. Tính thể tích khối lăng trụ.
Bài tập 5
Cho lăng trụ tam giác đều ABCA’B’C’ có cạnh đáy là a, chiều cao gấp đôi cạnh đáy. Gọi E và F lần lượt là trung điểm của các cạnh AA’ , BB’ . Tính tỉ số thể tích khối chóp C.ABEF và thể tích khối lăng trụ đã cho
Bài tập 6
Cho lăng trụ đứng tam giác ABCA’B’C’ có tất cả các cạnh đều bằng a. Tính thể tích khối tứ diện A’BB’C.
Bài tập 7
Cho khối lăng trụ đứng tam giác ABCA’B’C’ có đáy là tam giác vuông tại A với AC = b, góc ACB là 600. Đường thẳng BC’ tạo với mặt phẳng AA’C’C một góc bằng 300.
Tính độ dài đoạn thẳng AC’
Tính thể tích khối lăng trụ đã cho
Bài tập 8
Cho khối lăng trụ tam giác ABCA’B’C’ có đáy là tam giác đều cạnh a, điểm A’ cách đều 3 điểm A, B , C, cạnh bên AA’ tạo với mặt phẳng đáy một góc 600.
Tính thể tích khối lăng trụ đó
Chứng minh mặt bên BCC’B’ là hình chữ nhật
Tính tổng diện tích các mặt bên của hình lăng trụ tam giác ABCA’B’C’
Bài tập 9
Cho khối lăng trụ tam giác đều ABCA’B’C’. Gọi M là trung điểm của cạnh AA’. Mặt phẳng đi qua M, B’ , C chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó.
Hy vọng, với lượng thông tin trên đây sẽ giúp bạn củng cố lại kiến thức về lăng trụ tam giác đều. Chúng tôi xin chúc các bạn hoàn thành khóa học với kết quả tốt nhất nhé. Cảm ơn các bạn đã theo dõi bài viết trên.